| V I S U A L I Z Z A D I S C U S S I O N E |
| miss smile |
Inserito il - 18/06/2009 : 17:19:34
Premetto che la domanda è cretina, ma purtroppo non riesco a venirne a capo. La funzione in esame è:
(x - 1)
f(x) = ------------- (RAD5 = radice quinta)
RAD5(x^2 - 5)
Devo determinare il dominio e l'eventuale simmetria.
Essendo una funzione fratta, devo porre il denominatore diverso da zero. Ma trattandosi della radice con indice dispari, non è necessario che il radicando sia positivo, giusto?
Quindi la mia unica condizione è RAD5(x^2 - 5) diverso da zero.
Elevando entrambi i membri per 5, ottengo: x^2 - 5 diverso da zero, e quindi x diverso da ± RADQ(5). Il dominio quindi è tutto R tranne ± RADQ(5).
Tracciando il grafico della funzione con il programma Derive, ottengo invece un dominio diverso:
Immagine:
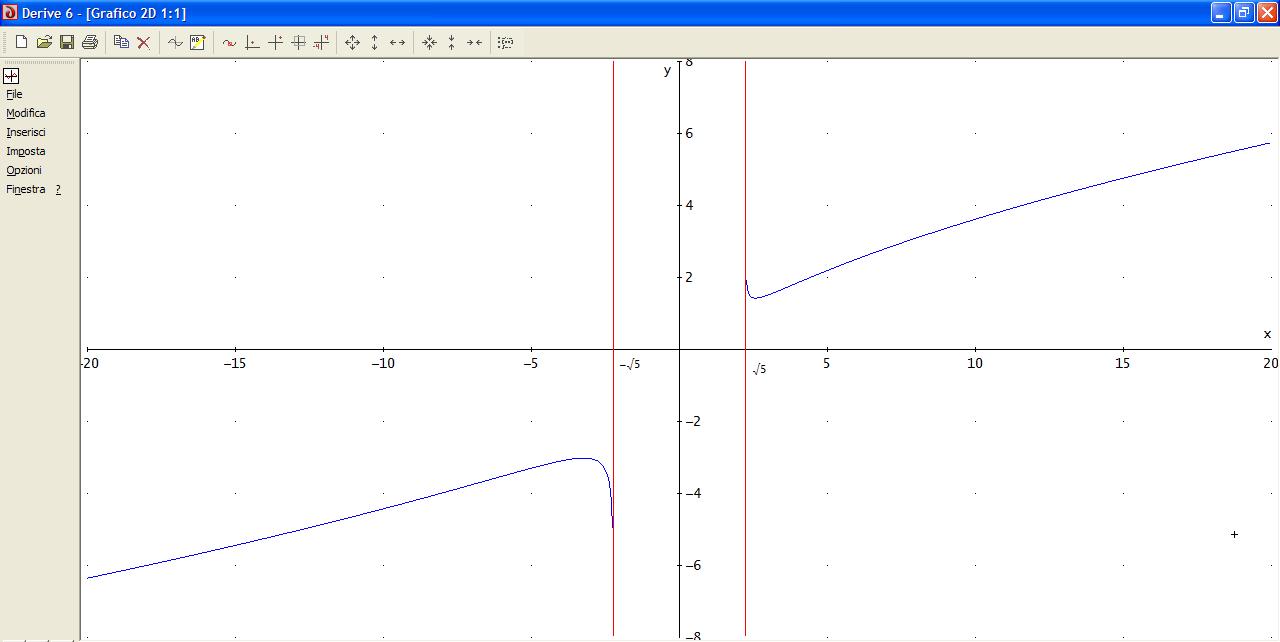
50,49 KB
Come si può vedere, l'intervallo ]-RADQ(5);RADQ(5)[ non appartiene al dominio. Perchè???
E poi, io non sono riuscita a trovare simmetrie (ragionando algebricamente), mentre dal grafico evince una simmetria dispari.
Qualcuno che mi chiarisca questi dubbi?? Grazie in anticipo. |
| 5 U L T I M E R I S P O S T E (in alto le più recenti) |
| miss smile |
Inserito il - 21/06/2009 : 09:23:05
Grazie mille Fra!  |
| Fra_221187 |
Inserito il - 20/06/2009 : 16:22:31
Si, dovrebbe darti lo stesso grafico, è il derive che non lo disegna correttamente. Se puoi cambia applicazione... |
| miss smile |
Inserito il - 19/06/2009 : 12:28:16
Fra, dici che è il mio programma che non va bene? 
Nel Derive non esiste la funzione della radice quinta, quindi ho dovuto scrivere la funzione cosi:
f(x) = (x - 1)/((x^2 - 5)^(1/5)), che poi dovrebbe essere equivalente, no? |
| Fra_221187 |
Inserito il - 19/06/2009 : 09:45:40
Grapher lo disegna così:
 |
| miss smile |
Inserito il - 18/06/2009 : 17:20:51
Per sicurezza, riscrivo la funzione: f(x) = (x - 1)/(RAD5(x^2 - 5)) |
|
|


